【位运算】801. 二进制中1的个数

  • 使用 lowbit 查找出二进制中 11 的个数
1
2
3
int lowbit(int x){
	return x & -x;//-x具有较高优先级
}

每次进行 lowbit ，然后减去 lowbit(x) 直到为 00。减的次数即为答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//学校垃圾评测机需要吸氧O3
#pragma GCC optimize(3)
#include <bits/stdc++.h>
using namespace std;

int main(){
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	int n;
	cin>>n;
	while(n--){
		int k,a = 0;
		cin>>k;
		while(k > 0) k -= (k&-k),a++;//内嵌lowbit
		cout<<a<<" ";
	}
}

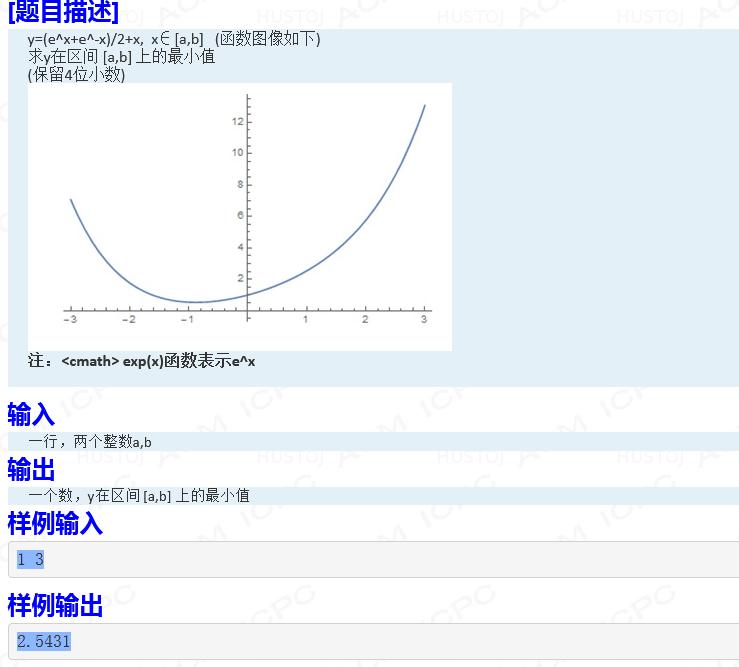
三分

点击展开题面

image

  • 直接套三分模版。
    如何求 lmid,rmidlmid,rmid :
1
2
double lm = l + (r - l) / 3.0;
double rm = r - (r - l) / 3.0;
  • Warning：需要求的是函数的yy 值！
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <bits/stdc++.h>
using namespace std;
const double eps = 1e-5;
double f(double x) {
	return (exp(x) + exp(-x)) / 2 + x;
}
int main() {
	double l, r;
	cin >> l >> r;
	while (abs(l - r) > eps) {
		double lm = l + (r - l) / 3.0;
		double rm = r - (r - l) / 3.0;
//		cout << lm << " " << rm << endl;
		
		if (f(lm) > f(rm)) {
			l = lm;
		} else {
			r = rm;
		}
	}
	cout << fixed << setprecision(4) << f(l);
}

哈希

  • 详见之前的blogs

朴素哈希（unordered_map）

【哈希表】840. 模拟散列表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//速通整活版
#pragma GCC optimize(3)
#include <bits/stdc++.h>
using namespace std;
const double eps = 1e-5;
unordered_map <int,int> mp;
int main() {
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	int q;
	char op;
	int x;
	cin>>q;
	while(q--){
		cin>>op>>x;
		if(op == 'I'){
			mp[x]++;
		}else cout<<((mp[x] == 0) ? "No" : "Yes")<<"\n";
	}
}

字符串哈希

  • 之前的博客有讲过。
  • 这次注意的点：在求 charchar 类型数组长度的时候如果下表从 11 开始就要写成 strlen(char+1) 而不是唐氏的 strlen(char)-1。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#pragma GCC optimize(3)
#include <bits/stdc++.h>
using namespace std;
const int P = 131;
char s[1000100];
unsigned long long/*!Important!*/ h[1010100], p[1010000];
void gethash() {
	int len = strlen(s+1)/*!Important!*/;
	p[0] = 1;//!Important!
	for (int i = 1; i <= len; i++) {
		p[i] = p[i - 1] * P;
		h[i] = h[i - 1] * P + s[i];
	}
}
unsigned long long get11(int l, int r) {
	return h[r] - h[l - 1] * p[r - l + 1];
}
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	int n, q;
	cin  >> n >> q>> (s + 1);
	gethash();
	for(int i = 1;i <= q;i++){
		int a,b,c,d;
		cin>>a>>b>>c>>d;
		if(get11(a,b) == get11(c,d)){
			cout<<"Yes\n";
		}else{
			cout<<"No\n";
		}
	}
}

二分

数的三次方根

  • tips: 这里不放标准解法了，水一发立方根函数 double cbrt(double x)。直接求 x 的三次方根。
1
2
3
4
5
6
7
#include <bits/stdc++.h>
using namespace std;
int main(){
	double x;
	cin>>x;
	cout<<fixed<<setprecision(4)<<cbrt(x);
}

P2678 [NOIP 2015 提高组] 跳石头

  • 题解见Here,这个写的很有实力
  • Warning：如果你过不了样例，可能是你二分的 ll 和输入的 ll 重名了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#pragma GCC optimize(3)
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5+10;
#define int long long
int n, m, d;
int a[50010];
bool check(int mid){
	int tot = 0,i = 0,now = 0;
	while(i < n+1){
		i++;
		if(a[i]-a[now] < mid) tot++;
		else now = i;
	}
	return tot <= m;
}
signed main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> d >> n >> m;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	a[n+1] = d;
	int l = 1, r = d,ans = 0;
	while (l <= r) {
		int mid = l + r >> 1;
		if (check(mid)) l = mid + 1,ans = mid;
		else r = mid - 1;
	}
	cout<<ans;
}

离散化

【离散化】802. 区间和

  • 一开始打桶排序前缀和的时候循环范围没设置好导致发生了一些TLE的莫名错误
  • 然后吸氧+关同步流过了一半，WA。
  • 然后数组开小了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#pragma GCC optimize(3)
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5+10;
#define int long long
int c[N], a[N], b1[N], b2[N], d[2*N]/*!!!Danger!!!: 至少3e5*/;
int ton[5 * N];
int k, n, q;
vector<int> v;
signed main() {
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	cin >> n >> q;
	for (int i = 1; i <= n; i++) {
		cin >> a[i] >> c[i];
		v.push_back(a[i]);
	}
	for (int i = 1; i <= q; i++) {
		cin >> b1[i] >> b2[i];
		v.push_back(b1[i]);
		v.push_back(b2[i]);
	}
	for (int i = 0; i < v.size(); i++) {
		d[i+1] = v[i];
	}
	sort(d + 1, d + 1 + v.size());
	k = unique(d + 1, d + 1 + v.size()) - d - 1;
	for (int i = 1; i <= n; i++) {
		a[i] = lower_bound(d + 1, d + 1 + k, a[i]) - d;
		ton[a[i]] += c[i];
	}
	for (int i = 1; i <= k/*!!!Danger!!!*/; i++) {
		ton[i] += ton[i - 1];
	}
	for (int i = 1; i <= q; i++) {
		b1[i] = lower_bound(d + 1, d + 1 + k, b1[i]) - d;
		b2[i] = lower_bound(d + 1, d + 1 + k, b2[i]) - d;
		cout<<ton[b2[i]]-ton[b1[i]-1]<<"\n";
	}
}