Bellman-Ford算法和SPFA学习笔记

Bellman-Ford

前置知识

• 首先你需要知道图论最核心的一个思路——松弛。
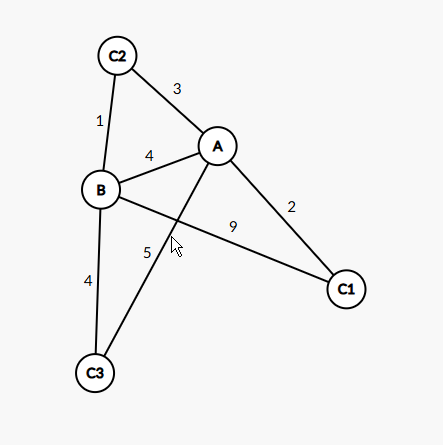
• 他是啥呢？笔者当时学的时候也花了亿堆时间理解它，就是假如我们现在有一些边，如图：
  简单来说，松弛就是不断的更新两个点的距离使得它比之前的答案更优。
  在这张图片里，我们将要松弛的 $2$ 个节点为 $(A,B)$ ，$A$ 为源点

那么它的原始距离是 $10$ ，那么如果我更新了他的一条路径（松弛成功），这个路径的边权和一定是要比 $10$ 小的。
好，那我们先来遍历和 $B$ 点有直接连边的节点。

• 先看 $C_1$ 那我们知道现在点 $C_1$ 到点 $A$ 的距离是 $2$ ，那因为 $C_1$ 到点 $B$ 的距离是 $9$ ，所以 $A$ 到 $B$ 经过点 $C_1$ 的距离就是 $2+9=11$ ，很显然，这个答案是比当前已知答案要差的。所以这次松弛并没有成功，我们选择放弃当前绕路的边权和。

• 再看 $C_2$ 那我们知道现在点 $C_2$ 到点 $A$ 的距离是 $3$ ，那因为 $C_2$ 到点 $B$ 的距离是 $1$ ，所以 $A$ 到 $B$ 经过点 $C_2$ 的距离就是 $1+3=4$ ，这时候我们发现，这个答案是比当前已知答案要优的。所以这次松弛成功，我们选择更新当前绕路的边权和为 $A\sim B$ 目前为止的最短路径。更新后的图如下：
  

• 最后看 $C_3$ 那我们知道现在点 $C_3$ 到点 $A$ 的距离是 $5$ ，那因为 $C_3$ 到点 $B$ 的距离是 $4$ ，所以 $A$ 到 $B$ 经过点 $C_3$ 的距离就是 $4+5=9$ ，很显然，这个答案是比当前已知答案要差的。所以这次松弛并没有成功，我们选择放弃当前绕路的边权和。

那么经过一轮松弛操作下来，我们最终所的结果就是——$A\sim B$ 的最短路为 $4$ 。

正题

如果你松弛理解好了，那么Bellman-Ford算法就是对于每一个点和源点进行松弛操作，如果答案更优，那么更新该点到源点的距离。
这样的松弛操作每次必然能确定 $\ge 1$ 个点的最短路。那么我们的BellmanFord算法的轮数就是 $n-1$ 轮。
换句话说，当一个有解的最短路使用BellmanFord求解时进行的 $\ge n$ 轮的操作都是没有意义的。那么如果该图无解呢？

判负环

• 如果一个有负环的图使用BF（BellmanFord）算法求解，每次进行一大轮的松弛都会导致更新，这会导致最短路随着轮数的增加越来越小，那么我们在用BF算法判断负环时只需要在 $n-1$ 轮结束后再进行一轮松弛，如果最短路变了，那么该图有负环！ 因为正常的图在第 $n-1$ 轮过后无论在如何松弛都会失败，而有负环的图每次松弛都能更新最短路长度。
• 貌似BF算法比别的算法的有点就只有这一个

时间复杂度

• 这个算法的时间复杂度巨巨巨好算，是 $O(NE)$ ,($N$ 是点数 $E$ 是边数)。

模板

/*Bellman-Ford算法板子*/
#include <bits/stdc++.h>
using namespace std;


struct edge {
	int to, nxt, l; //暴力存边
} e[1000001];
int n, m, s; //点，边，源点
long long d[1000001];//d[i]记录源点到点i的距离,longlong要开因为太小的话没法判断是否有解


int main() {
	memset(d,0x3f,sizeof d);
	scanf("%d%d%d", &n, &m,&s);
	d[s] = 0;//起点一定要初始化！
	for (int i = 1; i <= m; i++) {
		scanf("%d%d%d", &e[i].to, &e[i].nxt, &e[i].l);
	}
	for (int i = 1; i <= n - 1; i++) {
		//先整正常操作
		for (int j = 1; j <= m; j++) {
			if (d[e[j].to] + e[j].l < d[e[j].nxt]) d[e[j].nxt] = d[e[j].to] + e[j].l;
		}
	}
	for (int i = 1; i <= m; i++) { //开始判断负环
		if (d[e[i].to] + e[i].l < d[e[i].nxt]) {
			cout << -1;
			return 0;
		}
	}
	for(int i = 1;i <= n;i++){
		if(d[i] < d[0]/2) cout<<d[i]<<"\n";//有解
		else puts("NoPath");
	}
}

SPFA

• 对于上面的BF算法，我们会发现：在这一轮中每个店都要松弛，有好多店压根就没变，这岂不是太浪费时间了？！
• 那我们直接更新改变过的节点不就完了？！
• 他就是SPFA。我们把更改的节点入队，从队列中取节点进行松弛即可。

它死了

• 如果遇到节点巨巨巨巨稠密的图，SPFA会将一个节点入队入队入队入队——喜提TLE。
• 所以呢，如果没有负权边这边建议直接Dijkstra搞。

判断负环

• 如果一个点入队 $n$ 次，那么就代表它被松弛了 $n$ 次，即：有负环！

判断负环例题：P2850 [USACO06DEC] Wormholes G

/*体面意思就是，从任意一点出发，走一圈之后回到这个点路径长度总和小于零的路径是否存在，这不就是判断负环吗？！*/
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6+10;
int pre[N], k; //链式前向星
struct edge {
	int to, l, nxt;
} a[N]; //链式前向星
int dis[N];//点和源点的距离
int vis[N];//记录入队几次了（判断负环）
bool inqu[N];//记录元素是否在队列内部
int t, n, m, w;
queue <int> q;
void add(int u, int v, int w) {
	a[++k] = {v, w, pre[u]}, pre[u] = k;
}

void spfa() {
	while (!q.empty()) q.pop();
	//我们在一个点入队的时候检测他是不是松弛了n次
	vis[0] = 1;
	inqu[0] = 1;
	q.push(0);
	while (!q.empty()) {
		int hd = q.front();
		q.pop();
		inqu[hd] = 0;
		for (int i = pre[hd]; i; i = a[i].nxt) { //有向边我们要用队头节点扩展未确定的节点
			if (dis[hd] + a[i].l < dis[a[i].to]) {
				dis[a[i].to] = dis[hd] + a[i].l;
				//如果元素不在队列里面就push进去，避免重复push，因为队列中早晚轮到他，而且虽然队列没重新push但是对应的dis更新了
				if (inqu[a[i].to] == 1) continue;
				inqu[a[i].to] = 1;
				vis[a[i].to]++;
				if (vis[a[i].to] >= n) {
					cout << "YES\n";
					return ;
				}
				q.push(a[i].to);//服了这句没写又调了半小时。。。
			}
		}
	}
	puts("NO");
}

int main() {
	scanf("%d", &t);
	while (t--) {
		memset(vis, 0, sizeof vis);
		memset(inqu, 0, sizeof inqu);
		memset(pre, 0, sizeof pre);
		memset(dis, 0x3f, sizeof dis);
		k = 0;
		scanf("%d%d%d", &n, &m, &w);
		for (int i = 1; i <= m; i++) {
			int x, y, z;
			scanf("%d%d%d", &x, &y, &z);
			add(x, y, z); //双向建图 -> 调了半小时
			add(y, x, z);
		}
		for (int i = 1; i <= w; i++) {
			int x, y, z;
			scanf("%d%d%d", &x, &y, &z);
			add(x, y, -z); //时间逆转x等于时间流逝-x
		}
		dis[0] = 0;
		for (int i = 1; i <= n; i++) {
			add(0, i, 0);
		}
		spfa();
		//因为负环不一定从哪一个点走都能遇见，所以我们直接让0号节点和其他节点建边权为零的有向边（超级源点思想），这样就能跑到所有节点了，还不影响其他节点和总时间，最后跑一遍0-n的SPFA
	}
	
	
}