扫描线
摘自洛谷
扫描线算法是一种求矩形的面积并和周长并的好方法。其思想是由一条假想的线从图形的下方扫向上方(或者左方扫到右方,都可以),那么通过分析扫描线被图形截得的线段就能获得所要的结果。该过程可以用线段树进行加速(文字 from @NCC79601)
接下来,我将把扫描线分成面积并和周长并两个部分,尽量用非常通俗的语言和较为细致的步骤进行讲解
一、面积并
这一道题,就是面积并的模板题
既然是要我们求这几个矩形的覆盖面积,我们就来看一下,要是我们要求下面这个图形的覆盖面积,我们应该怎么做?
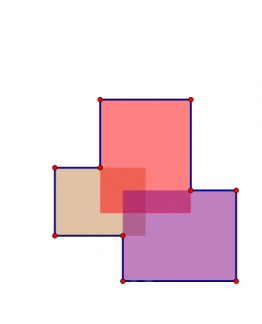
注意看,这里是有一部分的面积是重合的。所以说,我们要求的面积其实就是下面这个图:
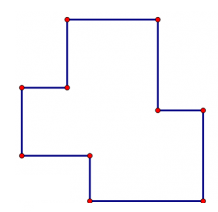
这个图形是一个不规则的图形,用什么方法求呢?
在初中数学中,我们求不规则图形的最普遍也是最简单的方法是什么?是割补法。所以,我们可以把这个图形进行割补:

这样子,我们就可以求出每一块分割后的图形面积来求出整个图形的总覆盖面积
我们可以用图象来模拟一下整个扫描线大概是怎么操作的,这里给出的是从左往右的模拟:

(以上图象均 from @Gu_Pigeon
)
观察上面这张 gif 不难看出,扫描线在扫的时候,似乎在扫到线段的时候就会把图形分割。那么,我们就看看,分割后的面积应该怎么求:
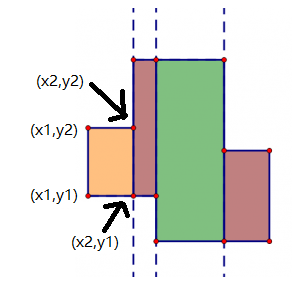
黄色那一块图象的左下角坐标为(x1,y1), 右上角坐标为(x2,y2), 那么左上角就为(x1,y2), 右上角即为(x2,y1)。这一块图象的面积就是(y2−y1)∗(x2−x1),我们后面要用这个式子来计算面积
现在我们来讲一下整个算法的一些操作
设立全局变量ans记录答案,读入x1,y1,x2,y2
首先要先把数据读进来
在读入之后,我们先得离散化
可不是嘛,看一下样例,0≤x1<x2≤ 109,0≤y1<y2≤ 109, 这个一看就会爆空间。所以我们要用芝麻换西瓜,牺牲小部分空间来离散化
然后我们要排序
既然我们是从左往右扫,那么最先扫到的那一条线段的 x 必然是最小的,所以我们就要让整个图象的线段进行排序,使得 x 小的线段可以先被扫到
我们还要运用线段树
先问一个问题:为什么要优化这个算法?
不难发现,我们在从左往右扫时,最难计算的其实就是扫到的那一条线段的长度。因为一条线段不一定是该矩形的边,比如这一条红色线段:
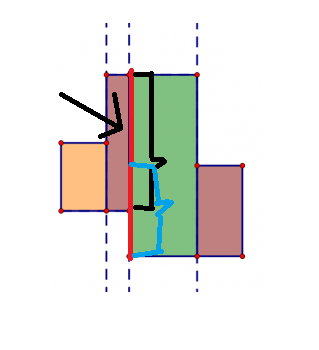
这一条线段,其实就是由黑色框起来的这一部分线段(这条线段是一个矩形的边)加上蓝色框起来的线段(这条线段也是一个矩形的边)再减去重合部分。因为这里只有三个图形,所以计算量也不大。但是,要是有更多的矩形像这样子重合,计算量就很大了,很浪费时间的。所以我们要用一些奇技淫巧来优化整个算法
再问一个问题,为什么要用线段树?
其实也已经很明显了。假如我们要求的是这一条红色的线段的长度,并不用把多个重合的矩形的边加到一起再减去重合部分,我们其实可以这样子算:
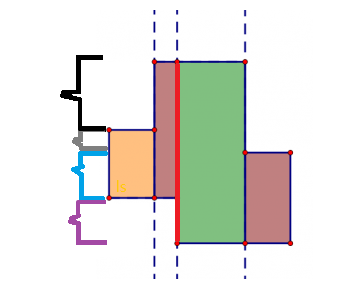
我们可以把黑色框起来的线段加上灰色框起来的线段加上蓝色框起来的线段加上紫色框起来的线段,得出这条红色线段的长度。而这些框起来的地方就是一条线段。那么,类似的,我们可以建立线段树,管理图中所有矩形的 y 坐标之间的线段。节点的特征值就是当前扫描到的线段在管理范围内的总长度
比如,我们定义tr[1]所管理的范围就是从图象最上面的 y到最下面的y,也就是管理黑色、灰色、蓝色和紫色框起来的这些线段。tr[1]的特征值c就是从图象最上面的y到最下面的y这个范围中包含被扫到的线段的长度。当扫到第一条线段的时候,只有灰色和蓝色部分才有这一条被扫到的线段的一部分,所以tr[1].c=灰色+蓝色这部分的长度;扫到第二条线的时候,tr[1].c=黑色+灰色+蓝色(因为黑色和灰色和蓝色才含有扫描到的线)的长度;扫到第三条线的时候,tr[1].c=黑+灰+蓝+紫(都有有扫描到的线的一部分)的长度。…
那么,求这一条被扫到的线段的长度,我们只要用线段树比较基础的区间求和就可以了
最后一个问题,怎么判断哪些区间包含当前扫到的线段
我们可以通过区间求和来计算出扫描线的长度,但是我们要计算哪一部分的线段呢?就像上一幅图,你怎么知道什么时候加的是灰色和蓝色部分,什么时候加的是灰色、蓝色和黑色部分,还有什么时候加的是灰色和蓝色和黑色和紫色部分呢?这个时候,我们要引进入边和出边
此入边出边非图论的入边出边。这里的入边,指的是一个矩形中第一条被扫到的线段;而出边,就是这个矩形第二条,也就是最后一条被扫到的线段
我们可以这样子去理解:扫描到一条入边意味着有一个矩形进入到扫描线扫描的区域里面,那么我们在计算面积的时候当然要加上这一部分;而扫描到一条出边也就意味着有一个矩形已经扫描完了,这个矩形也就不在扫描线扫描的区域以内了,所以这个时候,我们就不再需要这一部分了
我们设入边为1 ,出边为−1。每个节点设立一个变量tag,记录这个节点管理的区间是不是有当前扫描到的线段的一部分,判断有没有的依据是节点的tag是否>0。如果>0就说明包含了线段的一部分,=0就是没有包含,不可能出现<0的情况
这样一来,当我遇到一条出边时,就可以与之前一条入边加上的抵消掉。再根据tag的定义,判断这个节点所管理的范围是否包含被扫到的线段,有的话就加上
我们其实也可以根据个人喜好,可以设入边为2, 出边为−2或者入边为3,出边为−3等等,只要入边和出边互为相反数且入边值 >0 > 出边值的都可以(也可以入出边互为相反数且入边小于出边,但后面的操作就要修改一下了)
那么举一个例子模拟一下算法流程:
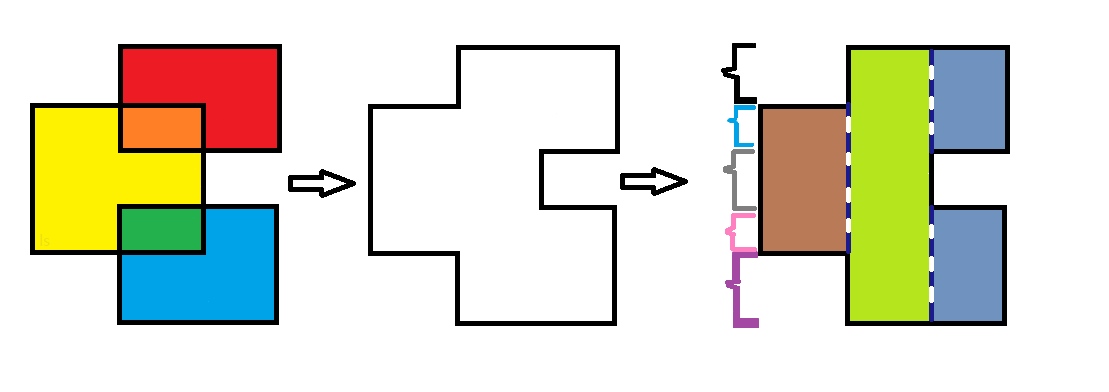
假设黑、蓝、灰、粉、紫所框起来的线段都为1,棕色矩形的宽为2,草绿色和灰蓝色矩形宽为1,开始模拟
扫到第一条边,是且肯定是入边。那么我们加上这一部分长度,刚好在蓝色、灰色和粉色区域,这三个区域tag都加1
当前各区域tag:
我们只计算tag大于0的区域的长度。所以ans=ans+ (蓝色+灰色+粉色) $ * $ 棕色矩形的宽 =0+(1+1+1)∗2=6
扫到第二条边,也是入边。所以黑色和紫色的区域tag加1
当前各区域tag:
同样计算tag大于0的区域的长度。ans=ans+ ( 黑色+蓝色+灰色+粉色$+紫色) * $草绿色矩形宽度 =6+(1+1+1+1+1)∗1=11
扫描到第三条边。这是一条出边。但是,这里只有灰色区域才含有这条出边,所以只有灰色区域的tag减1, 其它区域的tag不变
当前各区域tag:
现在灰色区域的tag等于0了,我们就不再需要计算灰色区域这一部分的长度,只计算其它区域的。ans=ans+(黑色+蓝色+粉色+紫色$)* 灰蓝色矩形宽=11+(1+1+1+1)* 1=15$
这里因为重叠了两条线段,所以这一幅图实际上只有四条线段。扫描到第三条线段时候其实已经宣告扫描结束了。因为最后一条线段是且肯定是出边,这条线段的后面也不可能再有面积覆盖, 而且扫描到最后一条线段所有的tag都会变成0。多计算这一步就略显冗杂。所以在面积并中,可以不用计算到最后一条线段
不用扫第四条边了,输出ans即可
给出这一幅图的数据吧:
输入:
1
2
3
4
| 3
0 1 3 4
2 3 4 5
2 0 4 2
|
输出:
至此,整个算法大概框架我们已经讲的差不多了,现在来讲一些小细节
细节 1:
根据上面的一些例子可以发现,在这里线段树维护的是线段,而不是一个个点。,每一个节点记录的是一整条线段,而不应该记录节点
那么,我们在修改tag还有区间求和的时候要怎么做?例如这幅图:

又放送
离散化以后,y坐标共5个,总区间为[1,5]。扫描到第一条边时,需要更改的区间为[2,4]。这里mid=(2+4)>>1=3。要是直接按线段树模板来修改的话,我们就将修改区间[2,3]和[4,4]
咦,怎么出现了[4,4]? 这是一个点啊?这不是一条线段啊?要是修改和查询区间[2,4]时,我们不应该修改查询区间[2,3]和区间[3,4]吗?
要是我们不采取一些操作,那么我们实际修改[2,4]的tag还有区间求和时,就只会修改和加上[2,3]这个部分,而会漏掉[3,4]这一部分。这样子当然是不对的
众所周知,区间里有n个点,就意味着区间有n−1条线段。我们不妨将区间[l,r]表示成[l,r+1], 也就是[l,r]实际上是区间[l,r+1]的线段
回到例子。要是这样子的话,我们修改[2,3], 实际上我们就是在修改[2,4], 因为[2,3]表示的其实是[2,4]废话。而我们修改到了修改[2,2]和[3,3]的时候,实际上也正是在修改[2,3]和[3,4],刚好能达到我们的目的
这样子的话,虽然还会出现修改查询区间[i,i]的情况,但是这实际是区间[i,i+1]。这样子也不再会出现记录节点的情况
所以,我们就采用这种方法,使得在修改和查询区间[l,r]的时候,我们实际上修改和查询的是[l,r−1],这样就可以解决这个问题了
这第一个细节,是我觉得比较重要的地方,应当重视
细节 2:
既然要用到区间查询,我们是不是应该要打懒标记呢?
其实不然,我们要的,只是tr[1].c,也就是整个图象包含的被扫到的线段的长度。所以,我们根本没有必要pushdown下放到各个节点。相反,我们应该pushup上放到根节点,不断维护这个根节点
好了,就讲这么多,下面给出代码(附带注释):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
| #include<cstdio>
#include<algorithm>
#define ri register int
using namespace std;
typedef long long ll;
ll ans;
ll n;
ll x1,x2,y1,y2;
ll y[210000];//用来离散化
struct smx
{
ll y1,y2,x,mark;
//y1,y2 表示这条线段上面的那个点和下面的那个点的 y 坐标
//这里的 x 在这里不会用到,只是用来排序而已
//mark 表示这条边是入边还是出边
}line[210000];
bool cmp(smx a,smx b){return a.x<b.x;}//以 x 坐标进行排序
struct node
{
ll l,r,lc,rc,c,tag;
//lc,rc 为左儿子和右儿子的编号
//tag 用来判断扫描线扫到下一条线段时还包不包括这个矩形
}tr[410000];ll len;
void bt(ll l,ll r)//建树
{
len++;int num=len;
tr[num].l=l;tr[num].r=r;tr[num].lc=tr[num].rc=-1;tr[num].c=tr[num].tag=0;
if(l==r)return ;
else
{
int mid=(l+r)>>1;
tr[num].lc=len+1;bt(l,mid);
tr[num].rc=len+1;bt(mid+1,r);
}
}
void pushup(ll num,ll l,ll r)
{
if(!tr[num].tag)//如果 tag=0
{
if(l==r)tr[num].c=0;//[l,r] 表示的是 [l,r+1], 所以这里的意思是如果 l==r+1,那么就意味着它是树最底下的叶子节点,它不会有儿子,又没有被线段覆盖,所以 c 为 0
else tr[num].c=tr[tr[num].lc].c+tr[tr[num].rc].c;//虽然这个节点没有覆盖,但它的子节点可能会被覆盖,所以加上自己的儿子节点
}
}
void change(ll num,ll l,ll r,ll k)//num 为节点编号,l、r 为修改范围,k 用来修改
{
if(l<=tr[num].l&&tr[num].r<=r)
{
tr[num].tag+=k;
if(tr[num].tag)tr[num].c=y[tr[num].r+1]-y[tr[num].l];//如果 tag>0 要加上。又因为这里的 r 其实是 r-1 的,但离散化的这个 y 数组却没有这种操作,所以要加 1
else tr[num].c=0;//tag=0 就不加
pushup(num,tr[num].l,tr[num].r);//维护
return ;
}
int lc=tr[num].lc,rc=tr[num].rc;
int mid=(tr[num].l+tr[num].r)>>1;
if(r<=mid)change(lc,l,r,k);
else if(mid+1<=l)change(rc,l,r,k);
else change(lc,l,mid,k),change(rc,mid+1,r,k);
pushup(num,tr[num].l,tr[num].r);//维护
}
int main()
{
scanf("%lld",&n);
for(ri i=1;i<=n;i++)
{
scanf("%lld%lld%lld%lld",&x1,&y1,&x2,&y2);
y[(i<<1)-1]=y1;y[i<<1]=y2;//离散化
line[(i<<1)-1]=(smx){y1,y2,x1,1};line[i<<1]=(smx){y1,y2,x2,-1};//记录线段
}
n<<=1;//一个矩形就有两条线段
sort(y+1,y+n+1);//离散化操作
sort(line+1,line+n+1,cmp);//按照 x 坐标的大小顺序来排序
int cnt=unique(y+1,y+n+1)-(&y[1])-1;//去重操作计算有多少个不同的 y,也就是这个图象有几个 y。因为区间 [l,r] 表示的是 [l,r+1],所以区间 [l,r-1] 实际上是 [l,r],所以总区间长度 cnt 要多减一个 1
bt(1,cnt);//建树
for(ri i=1;i<n;i++)//开始扫描,面积并中扫描到 n-1 条线段即可
{
y1=lower_bound(y+1,y+cnt+2,line[i].y1)-y;//当前这条线段的 y1 坐标的离散值 ,表示线段的 y1 是在线段树的第(离散值)个节点
y2=lower_bound(y+1,y+cnt+2,line[i].y2)-y-1;//当前这条线段的 y2 坐标的离散值,表示线段的 y2 是在线段树的第(离散值)个节点,同时为了实际上是求 [l,r], 所以我们要求的是 [l,r-1],所以这里要减 1
change(1,y1,y2,line[i].mark);//修改
ans+=tr[1].c*(line[i+1].x-line[i].x);//ans 记录当前扫到的面积
}
printf("%lld\n",ans);//输出 ans
return 0;
}
|
这个代码是从左往右扫的,可以自己尝试打一下从下往上扫的代码,其实和这个代码已经没什么两样了
我还打了一个版本,两个代码虽然看起来有点不一样,但思想是一致的:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
| #include<cstdio>
#include<algorithm>
#define ri register int
using namespace std;
typedef long long ll;
ll ans;
ll n;
ll x1,x2,y1,y2;
ll y[210000];
struct smx
{
ll y1,y2,x,mark;
}line[210000];
bool cmp(smx a,smx b){return a.x<b.x;}//排序
struct node
{
ll c,tag;
//tag 用来判断扫描线扫到下一条线段时还包不包括这个矩形
}tr[810000];
void pushup(ll num,ll l,ll r)
{
if(!tr[num].tag)
{
if(l==r)tr[num].c=0;
else tr[num].c=tr[num<<1].c+tr[num<<1|1].c;
}
}
void change(ll num,ll l,ll r,ll y1,ll y2,ll k)//这里的 l,r 是 num 的管理范围,y1、y2 是上一个代码的 l,r
{
if(y1<=l&&r<=y2)
{
tr[num].tag+=k;
if(tr[num].tag)tr[num].c=y[r+1]-y[l];
else tr[num].c=0;
pushup(num,l,r);
return ;
}
ll mid=(l+r)>>1;
if(y1<=mid)change(num<<1,l,mid,y1,y2,k);
if(mid+1<=y2)change(num<<1|1,mid+1,r,y1,y2,k);
pushup(num,l,r);
}
int main()
{
scanf("%lld",&n);
for(ri i=1;i<=n;i++)
{
scanf("%lld%lld%lld%lld",&x1,&y1,&x2,&y2);
y[(i<<1)-1]=y1;y[i<<1]=y2;
line[(i<<1)-1]=(smx){y1,y2,x1,3};line[i<<1]=(smx){y1,y2,x2,-3};
}
n<<=1;
sort(y+1,y+n+1);
sort(line+1,line+n+1,cmp);
int len=unique(y+1,y+n+1)-(&y[1])-1;
for(ri i=1;i<n;i++)
{
y1=lower_bound(y+1,y+len+2,line[i].y1)-y;
y2=lower_bound(y+1,y+len+2,line[i].y2)-y-1;
change(1,1,len,y1,y2,line[i].mark);
ans+=tr[1].c*(line[i+1].x-line[i].x);
}
printf("%lld\n",ans);
return 0;
}
|
貌似第二个代码要快一点
二、周长并
这一个就是周长并了
只要你看懂了面积并,周长并其实是很好理解的
由于这里求的是周长而不再是面积了,我们很容易想到就用面积并的方法从下往上扫一遍,然后从左往右扫一遍,每次扫到线段就用ans+=tr[1].c就好了
要是这样想的话,你就错了!
比如这一幅图:

双放送
还是假设黑、蓝、灰、粉、紫所框起来的线段都为1,棕色矩形的宽为2,草绿色和灰蓝色矩形宽为1
我们先从左往右扫。扫到第一条线段,ans=ans+tr[1].c=0+(1+1+1)=3。目前还没有任何问题
扫到第二条线段,ans=ans+tr[1].c=3+(1+1+1+1+1)=8?
???为什么ans会等于8? 从左往右扫的话,到第二条线段ans不应该是5吗?怎么回事?
发现没有?在扫到第二条边的时候,其它区间的tag也是>0的,所以我们多计算了一些部分
因为当前覆盖和先前覆盖的交集已经计算过,所以要减去,计算出来的结果就是ans要加的是abs(tr[1].c-上一次的tr[1].c)
但是,你谷出的数据非常毒瘤,我曾在讨论区发现这几个贴:测试数据是否有错?? 和 论某谷的玄学评测机,都反映出这个问题
这道题一共有六个测试点,但是有两个点非常毒瘤
比如第五个数据点,要是排序用的不是稳定排序 stable_sort(sort 是不稳定排序),虽然在本地输出的和样例答案一样,但在洛谷玄学评测机评测时答案会出错
而第六个数据点更加鬼畜,连输入顺序都卡,样例在此:
1
2
3
4
5
6
7
| Input:
2
0 0 4 4
0 4 4 8
Output:
24
|
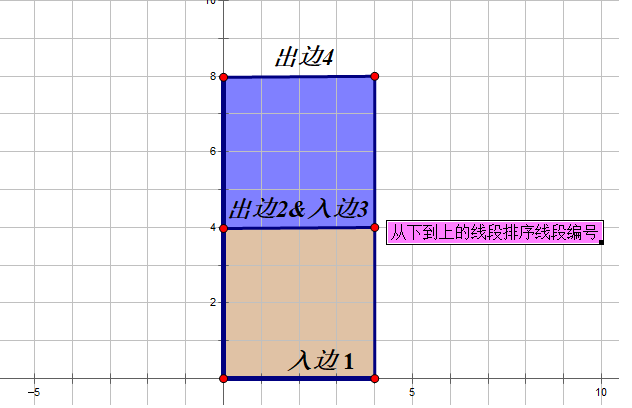
如图,可以发现出边2和入边3计算了2次,因为先扫到出边2,ans+=4;扫到入边3,ans又加了4,这样子得出来的答案就是32
有一个解决方法,可以A掉这两个数据点。当两条线段重合的时候,我们让入边先被扫描,再来扫描出边。这样子就可以不怕多计算周长了
还有最后一个小细节,周长并要遍历每一条线段,不像面积并一样遍历n−1条线段就可以
下面给出代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
|
#include<cstdio>
#include<algorithm>
#define ri register int
using namespace std;
int ans;
int n;
int x1,x2,y1,y2;
int x[11000],y[11000];
struct smx
{
int zb1,zb2,h,mark;
}line1[11000],line2[11000];
bool cmp(smx a,smx b)
{
if(a.h==b.h)return a.mark>b.mark;//重合时让入边先
return a.h<b.h;
}
struct node
{
int c,tag;
}tr1[41000],tr2[41000];
//下面这两个扫描线(从上到下,从左到右)框架基本一样,略显冗杂
void pushup1(int num,int l,int r)
{
if(!tr1[num].tag)
{
if(l==r)tr1[num].c=0;
else tr1[num].c=tr1[num<<1].c+tr1[num<<1|1].c;
}
}
void pushup2(int num,int l,int r)
{
if(!tr2[num].tag)
{
if(l==r)tr2[num].c=0;
else tr2[num].c=tr2[num<<1].c+tr2[num<<1|1].c;
}
}
void change1(int x1,int x2,int k,int num,int l,int r)
{
if(x1<=l&&r<=x2)
{
tr1[num].tag+=k;
if(tr1[num].tag)tr1[num].c=x[r+1]-x[l];
else tr1[num].c=0;
pushup1(num,l,r);
return ;
}
int mid=(l+r)/2;
if(x1<=mid)change1(x1,x2,k,2*num,l,mid);
if(mid+1<=x2)change1(x1,x2,k,2*num+1,mid+1,r);
pushup1(num,l,r);
}
void change2(int y1,int y2,int k,int num,int l,int r)
{
if(y1<=l&&r<=y2)
{
tr2[num].tag+=k;
if(tr2[num].tag)tr2[num].c=y[r+1]-y[l];
else tr2[num].c=0;
pushup2(num,l,r);
return ;
}
int mid=(l+r)/2;
if(y1<=mid)change2(y1,y2,k,2*num,l,mid);
if(mid+1<=y2)change2(y1,y2,k,2*num+1,mid+1,r);
pushup2(num,l,r);
}
int main()
{
scanf("%d",&n);
for(ri i=1;i<=n;i++)
{
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
x[(i<<1)-1]=x1;x[i<<1]=x2;
y[(i<<1)-1]=y1;y[i<<1]=y2;
line1[(i<<1)-1]=(smx){x1,x2,y1,1};line1[i<<1]=(smx){x1,x2,y2,-1};
line2[(i<<1)-1]=(smx){y1,y2,x1,1};line2[i<<1]=(smx){y1,y2,x2,-1};
}
n<<=1;
sort(x+1,x+n+1);sort(y+1,y+n+1);
sort(line1+1,line1+n+1,cmp);
sort(line2+1,line2+n+1,cmp);
int len1=unique(x+1,x+n+1)-(&x[1])-1;
int len2=unique(y+1,y+n+1)-(&y[1])-1;
for(ri i=1;i<=n;i++)//要遍历每一条线段
{
int t;
t=tr1[1].c;//记录上一次覆盖长度
x1=lower_bound(x+1,x+len1+2,line1[i].zb1)-x;
x2=lower_bound(x+1,x+len1+2,line1[i].zb2)-x-1;
change1(x1,x2,line1[i].mark,1,1,len1);
ans+=abs(tr1[1].c-t);
t=tr2[1].c;//同上
y1=lower_bound(y+1,y+len2+2,line2[i].zb1)-y;
y2=lower_bound(y+1,y+len2+2,line2[i].zb2)-y-1;
change2(y1,y2,line2[i].mark,1,1,len2);
ans+=abs(tr2[1].c-t);
}
printf("%d\n",ans);
return 0;
}
|